The Field of Two Antennas

Controlling the Pattern

Up to this point we have considered only the radiation from a vertical antenna system which contains just one radiating element. An antenna of this sort radiates equally well in all horizontal directions and so is referred to as an omnidirectional antenna. There are many instances, however, in which it is desirable to control the shape of the horizontal radiation pattern, so that the radiated signal may be reduced in strength in some directions and made particularly strong in others. In the operation of a standard AM broadcast station, for instance, it may be required that the radiation be severely limited in the direction of another station some distance away which has been assigned the same frequency of operation, so that interference will not be caused within the service area of the other station. At the same time, this will allow energy which is not being radiated toward the distant station to be diverted toward some area which the station is intended to serve. An arrangement which is capable of doing this is called a directional antenna system. Broadcast directional antennas can be designed and adjusted with great accuracy, so that they can produce radiation patterns which conform very closely to the theoretical values.

These directional effects are achieved by the use of two or more individual vertical antennas, each with its separate radial ground system and coupling network, spaced some portion of a wavelength distant from one another, and each driven in a definite current and phase relationship with respect to the others. An almost endless variety of radiation patterns may be obtained by variation of these quantities. The computation of the radiation pattern which will be produced by a given arrangement of towers and distribution of current and phase is often tedious, but it is not especially difficult mathematically.

Interfering Waves

Let us start with the arrangement shown in Fig. 48-1. Here we are looking downward upon two vertical antennas which are spaced ½ wavelength, or 180^o, apart at the operating frequency. These towers are of equal height, and the transmission lines and coupling networks have been so arranged that the currents in the two towers are equal in both magnitude and phase. Each tower is therefore the source of an electromagnetic wave, and these waves are equal in intensity and are in phase with each other as they leave the towers.

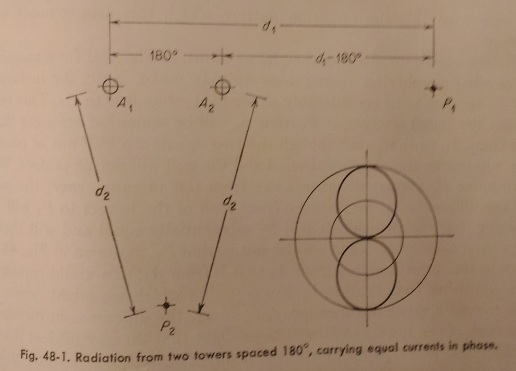
At the surface of the earth, some distance away from the towers, we have chosen two points, P₁ and P₂. P₁ is located in a direction which is in line with the towers, and P₂ is in a direction 90^o away from the line of the towers. We are referring to the towers as A₁ and A₂. Now we notice that it is the same distance from A₁ to P₂ as it from A₂ to P₂. Thus the waves which are radiated from the two towers are in phase with each other as they arrive at P₂ , so that they add to give twice the amplitude that would be present if one of the towers were removed from the system, leaving the current unchanged in the other tower. In the direction of P₁ , however, the situation is entirely different; the distance from A₂ to P₁ 180^o shorter than that from A₁ to P₁. At P₁ , then, the wave arriving from A₂ is leading the wave from A₁ by 180^o. The two waves therefore cancel each other in this direction, thereby producing a null in the radiation pattern. The same situation occurs along the line of towers in the direction opposite to that of P₁, , so that the resultant pattern of radiation contains two nulls, as indicated by the polar plot in Fig. 48-1.

But the information which we obtain from this sort of reasoning is not adequate to tell us the shape of the radiation pattern. We need to be able to determine the relative intensity of radiation in any direction around the antenna; furthermore , we should be able to accommodate in our computations any possible arrangement of spacing , phasing, and current ratio which we may wish to use. In order to do this, we must set up an equation which will express the relative field intensity in any direction as a function of these parameters. This will then allow us to select a certain arrangement of towers, current, and phasing and to compute from this the radiation pattern which this arrangement will produce.

Before setting up this equation, let us return to FIG. 48-1 for a moment to see what simplifying assumptions we may make. Note, for instance, that P₁ appears to be considerably closer to A₂ than it is to A₁. This tell us that the signal arriving at P₁ from A₂ will be somewhat stronger than that from A₁, so that, even though the two signals are 180^o out of phase, they will not be completely canceled and the null will not be perfect. But if we move P₁ a great distance away from the antenna array, the percentage difference in the distance from each towers to P₁ will be so slight that the two signals will be substantially equal and will therefore cancel each other. Then we also notice that P₂ , as drawn in Fig 18-1, is not in the same direction from A₁ as it is from A₂; this would certainly be a confusing complication in any equation which we might write. If P₂ is moved a great distance away, however, the difference in direction from each of the tower to P₂ will be so slight that we may neglect it and consider the point to be in the same direction as viewed from either tower. Our assumption, then, is that we are interested only in the radiation pattern as it appears at distances which are large in comparison with (10 times or more) the spacing between the towers.

For our purposes, this assumption is a valid one. There is usually no reason for use to concern ourselves with the radiation pattern in the immediate vicinity of the antenna system; it is the shape of the pattern at great distances that determines the usefulness of the antenna system as far as its communication value is concerned. The radiation pattern at distances which are relatively close to the antenna is confused and meaningless, so that field measurements taken in this region are quite misleading.

Vector Addition

The field intensity which will be produced in any given direction will be found by adding vectorially the separate field from the two radiating elements. This means that we must consider both the magnitude and the phase of each wave as it arrives at a point in the direction of interest. As far as the magnitude is concerned, we are assuming that the distances are equal from each tower to the point in question, so that the two arriving fields will have intensities which are simply proportional to the currents in their respective towers (provided, or course, that the towers are equal in effective height). With regard to the phase, however, we definitely must take into account the difference in distance from each tower to the point, for regardless of the total distance, 1^o difference in the distances will make 1^o difference in the relative phase of the fields as they arrive at the point: one is the current phasing , which is the phase relationship between the currents in the two towers, and the other is the space phasing, which is the difference in distance (expressed in electrical degrees) from each of the towers to the point in question. The equation which we write must take these factors into account automatically, regardless of the direction of the point with respect to the line of towers.

Let us now examine Fig. 48-2. Here we have the plan view of a two tower array, seen as though we were looking down upon the array from above. The towers, indicated as A₁ and A_2,, are spaced apart by a distance of S. We are interested at this time, not in the actual antenna currents or in the amount of power being fed to the antenna, but only in the shape of the radiation pattern; therefore we select one of the towers (say A₁) and arbitrarily state that it is carrying a current in A₁ and written B/φ, meaning that its magnitude is B times the current magnitude of A₁ and that it is leading the current in A₁ by φ. The point P is at some great distance; we don’t particularly care how far away it is, except that we must assume that it stays the same distance away as we move it around the array. The direction of the point P is the variable ϴ, measured from a line originating at A₁ and passing through A₂.

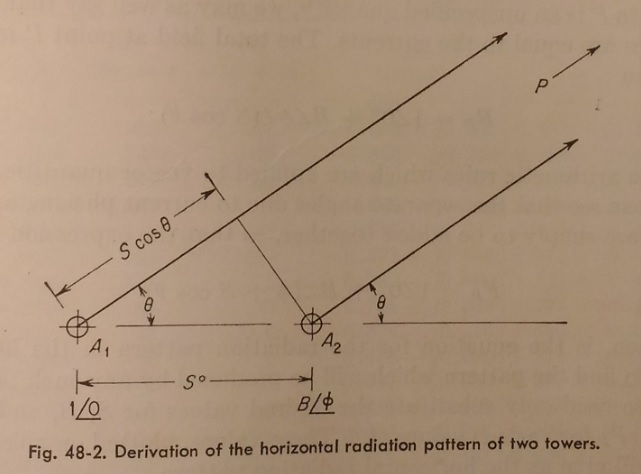
Let us now examine Fig. 48-2. Here we have the plan view of a two tower array, seen as though we were looking down upon the array from above. The towers, indicated as A₁ and A₂, are spaced apart by a distance of S. We are interested at this time, not in the actual antenna currents or in the amount of power being fed to the antenna, but only in the shape of the radiation pattern; therefore we select one of the towers (say A₁) and arbitrarily state that it is carrying a current in A₁ is 1/0^o . The current in A₂ is then stated with respect to that in A₁ is 1/0^o. The current in A₂ is then stated with respect to that in A₁ and written B/φ , meaning that its magnitude is B times that current magnitude of A₁ and that it is leading the current in A₁ by φ. The point P is at some great, distance; we don’t particularly care how far away it is, except that we must assume that it stays the same distance away as we move it around the array. The direction of the point P is the variable ϴ, measured from a line originating at A₁ and passing through A₂.

From the geometry of Fig. 48-2 and from the trigonometric relations described in Chap6.6, we can see that A₁ is farther from the point P than is A₂ by amount equal to the spacing S times the cosine of the angle ϴ. This relation will be true regardless of the value of ϴ. Thus the space phasing of the field from A₂ is such that it leads the A₁ field by an angle of Scosϴ. The current phasing of the A₂ field is of course the angle φ.

Since the field intensities are proportional to the currents and the distance to P is an unspecified quantity, we may as well say that the field intensities are equal to the currents. The total field at point P may then be written

F_P = 1/0^o + B/φ /(S cos ϴ)

From the arithmetic rules which are applied to vector quantities (Chap. 14), we can see that the separate angles due to current phasing and space phasing are simply to be added together, so that the expression becomes

F_P = 1/0^o + B/(φ + S cos ϴ)

This, then, is the equation for the radiation for the radiation pattern in the horizontal plane. To find the pattern which will be produced by any such two-tower array, we need only substitute the desired values for S, B, and φ, then compute F_P for various values of ϴ. These values, plotted on polar coordinates, will give us horizontal radiation pattern.

As an example, let us go through the computation and plotting of a typical two-tower directional antenna pattern. We shall assume that the spacing between the towers is 250^o and that the current in A₂ with respect to that in A₁ is 0.9/(-50^o + 250^o cos ϴ)

The pattern of array of this type will always be symmetrical about the line of towers; there is nothing in the arrangement which can cause the pattern on one side of the line of towers to be different from the pattern on one side of the line of towers to be different from the pattern on the other. Consequently, it is only necessary that we compute F_P f for values of ϴ between 0 and 180^o and 360^o, we shall find that the value of F_P is the same as for the corresponding angle between 0 and 180^o. The value of F_P for 290^o (which is the same as -70) will be equal to that for 70^o.

Organizing the Computation

The computations are best organized in tabular form. Proceeding in this manner in Table 48-1, we write in column 1 the angles at which we wish to compute the radiation. Here we have chosen to compute a value for each 10^o around the antenna. In column 2 we write the value of the cosine for each angle listed in column 1, nothing particularly the fact that the cosine value becomes negative for angles between 90 and 270^o.. To obtain the figures in column 3, we multiply the cosine values by 250^o, which gives us the space phasing in each direction.

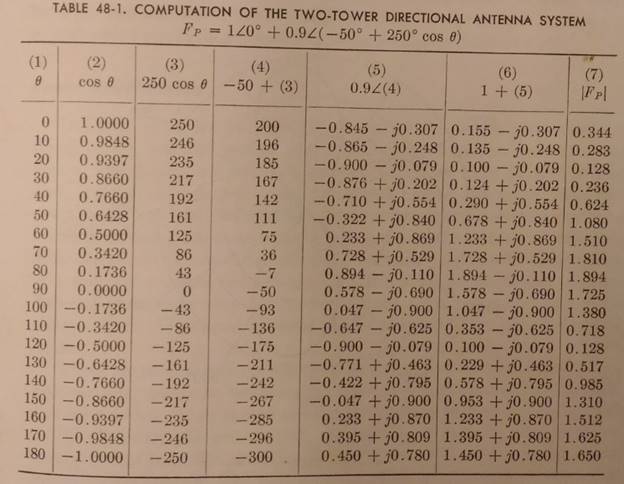
Next we add the current-phasing angle of -50^o to the values in column 3 to obtain the total phase angle between the two fields; this gives us column 4. The field magnitude 0.9 of A₂ at this last angle (4) gives us the vector contribution of the radiation from A₂ to the total field; this we must convert into rectangular form, producing the values in column 5. Then to these values we add 1 + j0, the field contribution from A₁, to obtain the total field values of column 6. But we cannot use directly these rectangular components of the composite field; we need to know the magnitude. Accordingly, we covert the complex values of column 6 into polar form. The value of the angle which we obtain as a part of this number is of no importance to us, as we do not especially care about the relative phase of the total field in various directions. We therefore do not even bother to write down the angle associated with each value of F_P; we give only the magnitude, as indicated by the symbol at the head of column 7.

Polar Plotting

Now that we have the field magnitude in each direction, we may plot the radiation in polar coordinates. Fig 48-3 shows the radiation pattern which results from the particular spacing, phasing, and current ratio which we have assumed. Since the currents in the two towers are not equal, there is no direction in which the fields of the two towers cancel completely. The intensity of radiation in the null directions, therefore, does not becomes zero but simply drops to a minimum value. Imperfect nulls such as these are broader in angle than those in which cancellation is complete and are therefore not quite so critical in adjustment when the antenna is being tuned. Also, by allowing a lobe of radiation to form around the direction of 0^o but purposely keeping it small, we may be able to keep the radiation below some maximum allowable value over the entire range of 330 to 30^o azimuth, which is equivalent to producing a null that is 60^o wide in the pattern. Devices such as these are often used by the designers of directional antenna systems in order to satisfy particular pattern requirements.

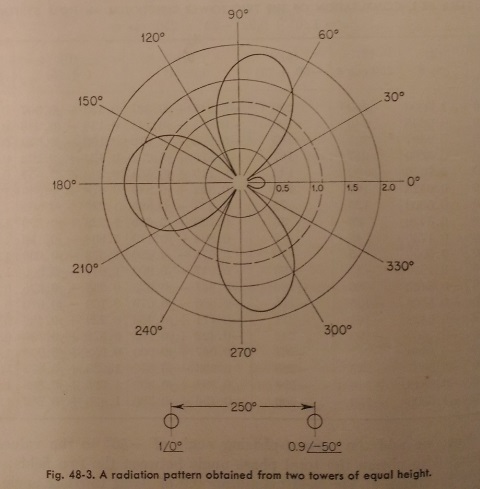
Thus far we have not said anything about determining the actual field intensity, expressed in millivolts per meter at 1 mile, which this directional antenna will produce with a given amount of radiated power. We have computed and plotted some relative values of F_P which tell us that the field becomes 1.9 at some angle between 70 and 80^o, and a gain between 280 and 290^o; but we must be able to express this in terms of actual signal strength. Fortunately, this is not too difficult a job.

Power Relationships

In Chap. 42 we learned that the area of a radiation pattern is proportional to the radiational power. This means that, if we can determine the area of the directional radiation pattern which we have plotted in Fig. 48-3, we can superimpose upon it a circle having the same area; this circle would be the radiation pattern of an omnidirectional antenna which is radiating the same amount of power and field of the directional antenna may easily be obtained from the ratios of the F_P values of the directional pattern to the radius of the omnidirectional circle.

There are several ways of determining the area of the directional radiation pattern; it may be measured by the use of a planimeter ( a small instrument which, when moved around the contour of a closed curve, will indicate directly the area within the curve), it may be computed by mathematical formulas ( a rather involved process), or it may be determined by transferring the pattern to a sheet of rectangular-coordinate paper and counting the pattern to a sheet of rectangular-coordinate paper and counting the squares and fractions thereof which are within the pattern. In any event, care must be taken to ensure that the area is measured in the same unit as is used on the radial scale of the polar plot or, if this is not done, that the proper correction is made.

Measuring the area of the radiation pattern of Fig. 48-3, we find that its value is 4.47 square units. Since the area of a circle is given by A = πr², the square of the radius of a circle of this same area will be 4.47/, or 1.42, and the radius will be 1.19 units. We therefore draw a circle of this radius on the directional- pattern plot; this is the dashed circle appearing in Fig. 48-3.

Now, let’s suppose that the towers have an over-all height of 90^o and that the power fed to the antenna is 5 kw. A single tower of this height will produce a field of 196 mv/m at 1 mile with 1 kw, or 438 mv/m at 1 mile for 5 kw. Therefore, the radius 1.19 of the dashed circle represents a field intensity of 438 mv, and the maximum radius of 1.9 of the directional pattern represents 438(1.9/1.19), or 700, mv/m at 1 mile. The field radiated in any direction by the directional antenna can thus be quickly computed by this procedure.

An occasion may arise wherein it is necessary to have towers of unequal height in a directional array. In this case, the field-intensity ratio of A₁ and A₂ will not be equal to the ratio of antenna currents. Both the field at 1 mile for 1 kw and the antenna base current for 1 kw will be different for towers of different heights; since it is the field ratio, rather than the antenna current, that is the important factor in determining the directional pattern, we must compute the current ratio required to produce the desired field-intensity ratio.

Suppose, for example, we wish to use one tower which is 90^o high and one which is 135^o high. The 90^o tower will produce 196 mv/m at 1 mile with 1 kw radiated, while the 135^o tower will produce 213 mv/m at 1 mile when radiating the same power. Since power varies as the square of the field intensity, we shall have to cut down the power in the taller tower to 846 watts to bring its 1-mile field down to equal that of the shorter tower. But the base resistance of the 90^o tower will probably be about 40 ohms, while that of the 135^o tower may be some 300 ohms. The current at the base of the shorter tower for 1 kw will therefore be 5.0 amp, while that at the base of the taller tower for 846 watts will be 1.68 amp. Thus, for equal fields from these two towers, the base-current ratio will be 5.0:1.68, or approximately 3:1, with the larger current being in the shorter tower. Field ratios other than 1:1 would then be achieved by appropriately modifying this current ratio.

Vertical Patterns:

Looking again at Fig 18-2 , let us imagine that we are viewing the antenna system from the side, rather than from above, and that the vertical lines which are drawn through the circles A₁ and A₂ represent the actual antenna towers. The angle marked θ we shall now call V; it is now the vertical angle above the horizon indicating the direction of a point P which is located high above the horizon, because it is this high-angle radiation pattern at such angle above the horizon, because it is this high-angle radiation which will be propagated to great distances by ionospheric reflection; the interference capabilities of this sky wave are often of great importance in determining the best antenna arrangement. We did not have to make much of a change in Fig. 48-2 to obtain a picture of the conditions at angles above the horizon, nor is any serious change in concept involved when we write the necessary equations. The space phasing, at least off the end of the array where we are looking at it (θ =0^o), is given by the factor S cos V, and we could, with this change of θ to V, go ahead and write the equation for the vertical pattern in this direction just as we did for the horizontal pattern, except for one important difference: we must not forget that the towers themselves have a vertical radiation pattern that is characteristic of their height, as shown in Figs. 42-2 to 42-4.

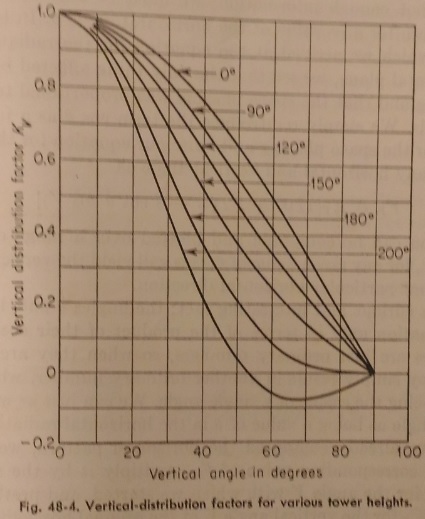
The vertical distribution of energy that is due to the towers themselves modifies the distribution that is due to the space phasing and the current ratio and phasing, so that it must be accounted for in writing the equation. This is conveniently done by establishing a quantity known as the vertical-distribution factor, which we shall call K_v. This is the proportional radiation at a vertical angle V, referred to the radiation in the horizontal direction. The expression which gives the value of radiation intensity as determined by the phasing, etc., will then be multiplied by K_v to make this necessary correction.

A chart showing the values of K_v for various vertical angles and for towers of various heights will be found in Fig. 48-4. Notice, for instance (and compare Fig. 42-2), that the intensity of radiation from a quarter wave (90^o) antenna at a vertical angle of 40^o is 0.7 times its intensity in the horizontal direction, while that from a half-wave (180^o) tower at the same vertical angle is 0.36 times its horizontal intensity.

So the radiation in the direction θ = 0^o at various values of the angle V above the horizon will be given by the equation

F_P = K_V[1/0^o + B/(∅ + S cos V)]

This still is not enough information; we must be able to compute the vertical pattern for any value of the horizontal angle θ. In looking over the way in which we arrived at the equation for the radiation pattern in the horizontal plane, we arrived at the equation for the radiation pattern in the horizontal plane, we see that the only thing affected by θ was the space phasing and that the space phasing was proportional to the cosine of θ. It still is. We simply reintroduce the term cos θ as a factor in the expression for the space phasing and write our equation for the radiation intensity at any horizontal and vertical angle as

F_P = K_V[1/0^o + B/(∅ + S cos θ cos V)]

This equation can be computed and plotted over a range of V values from 0 to 90^o, for any given value of θ; this will yield the vertical radiation pattern in that particular horizontal direction.

Here is a curious and interesting fact: the angle θ and V appear in this last equation only in terms of the product of their cosines. These cosine values are just ordinary numbers, so when they are multiplied together, they simply result in another ordinary number, which we can think of as being the cosine of a single angle. We can just as well consider this single angle as being a value of θ in the horizontal radiation pattern, so if we have already computed the horizontal pattern, we need only look up the corresponding value of F_P, multiply it by the appropriate value of K_V for the angle V with which we started, and presto! We have the value of F_P for vertical angle V at the original horizontal direction θ. This is very nice, because it means that, once the horizontal-plane pattern has been computed , no further vector computations need to be performed to obtain any or all of the vertical patterns. This procedure is valid not only for the two-tower array which we have been discussing but also for an array of any number of towers where the towers are all of equal height and are located in the same straight line.

As an example of this process, let us compute the radiation in the horizontal direction θ = 150^o and at the vertical angle of 20^o in the horizontal direction θ = 150^o and at the vertical angle of 20^o in the antenna array of Fig. 48-3. The cosine of 150^o is -0.8660, and the cosine of 20^o is 0.9397; these multiplied together give -0.814. Reference to a trigonometric table shows that this number is the cosine of 144.5^o. Looking at the horizontal pattern of Fig. 48-3, we see that the value of F_P corresponding to 144.5^o is 1.16. If the towers are assumed to be 90^o in height, we look on the vertical-distribution-factor chart of Fig. 48-4 for the value of K_v for a 90^o tower at a vertical angle of 20^o; this we find to be 0.915. Multiplying 1.16 by 0.915, then obtain a value of 1.061 for F_P at θ = 150^{o, ,} V = 20^o.

Vertical patterns are customarily plotted in polar coordinates, using, of course, only the portion of the coordinate system between 0 to 90^o. One such plot is made for each horizontal direction in which the vertical pattern characteristics will be of interest. Vertical patterns of directional antenna systems will often contain nulls and high-angle lobes, even when the towers are so short that their individual vertical patterns do not contain nulls. The vertical pattern in the 150^o direction for the antenna of Fig. 48-3 contains a null. Can you determine at what vertical angle it occurs?

By holding the value of the vertical angle V constant while varying the azimuth angle θ through the range of 0 to 360^o , we obtain a complete azimuthal pattern at the angle V above the horizon. Recent rules of the FCC have required that such a pattern be calculated for each 5^o of vertical angle up to 60^o for broadcast directional antennas in cases where the sky-wave radiation is an important factor in the allocation of the station.